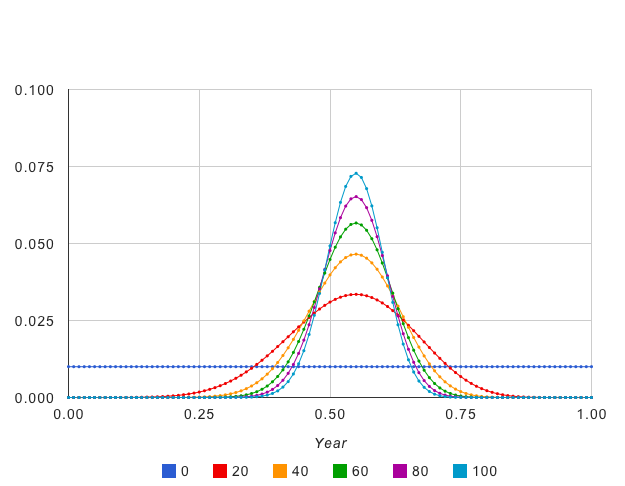
まずは、数理モデルとはどういうものかを、比較的計算量の小さいもので試してみましょう。今すぐに実行できるように作成しているので、プログラミングの知識も必要ありませんし、ダウンロードも必要ありません。ページを開くだけです！

大きく分けて３種類のモデルに分けられています。一つ目は個体群の人口論についてのモデルです。簡単に言うと、生物の個体数の増え方を数式で表すとどうなるか、というものです。二つ目はどのような行動をとる生き物が生き残りやすいのか、どのような遺伝子が次世代に伝わり、次世代に伝わりにくい遺伝子はどんなものか、というような進化についてのモデルです。三つ目は細胞の集合過程やブラウン運動など幾何的な側面をもつモデルです。

個体数の変化

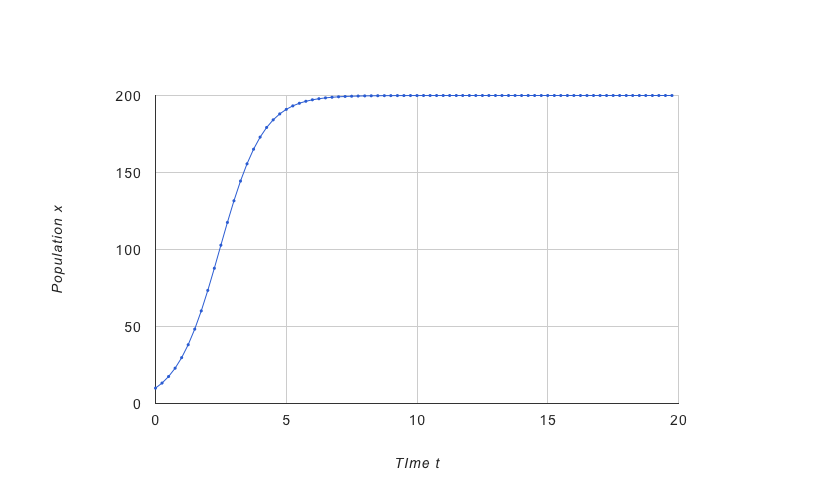
単一種の動態

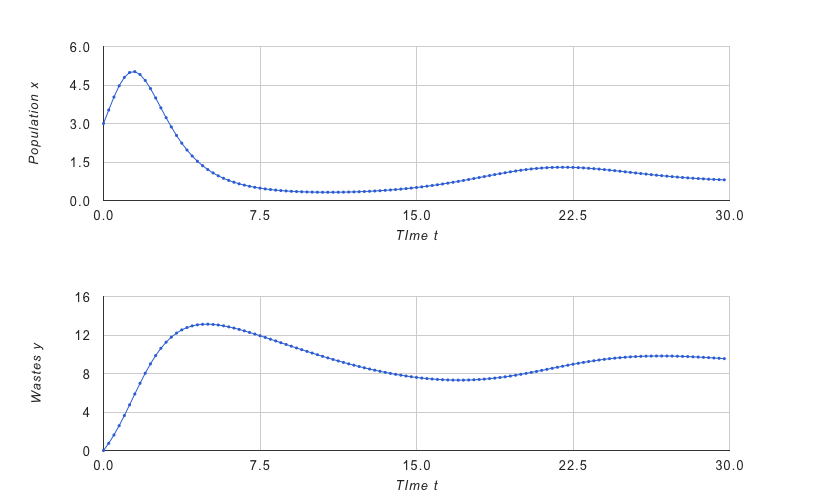
2種間の相互作用があるときの動態

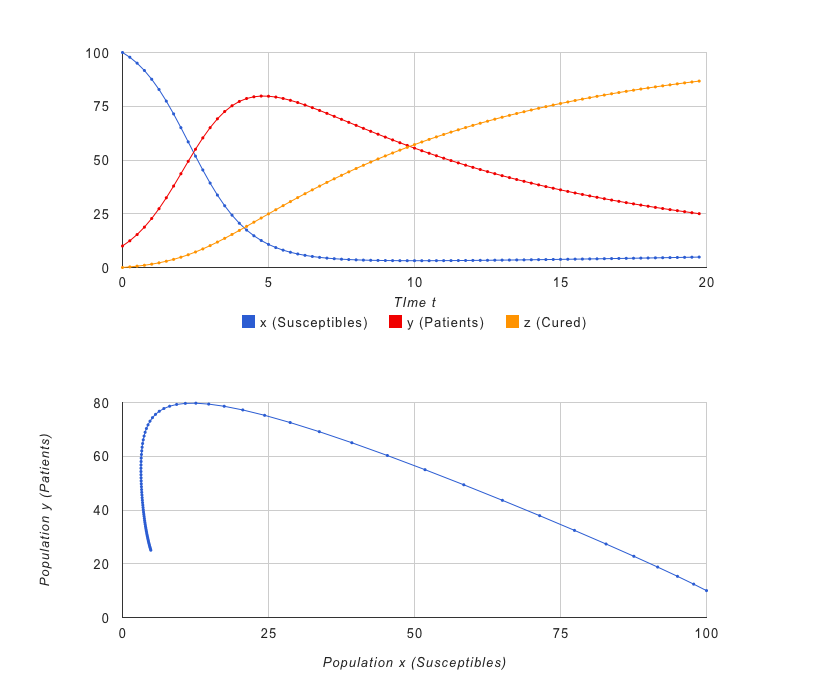
感染症モデル

離散時間モデル

進化モデル

進化的安定戦略(ESS)

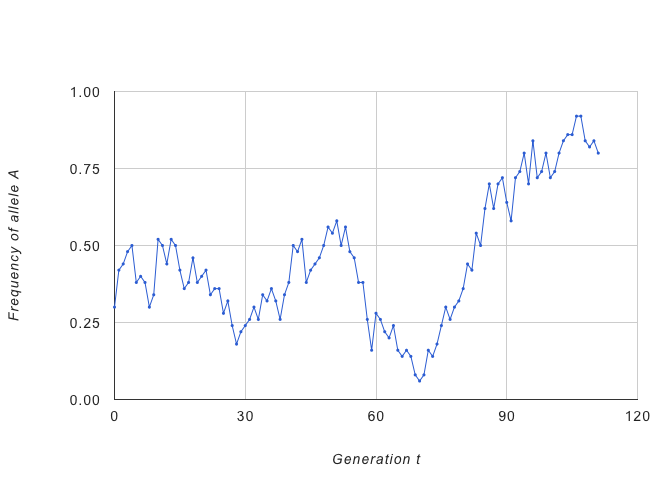
遺伝子頻度

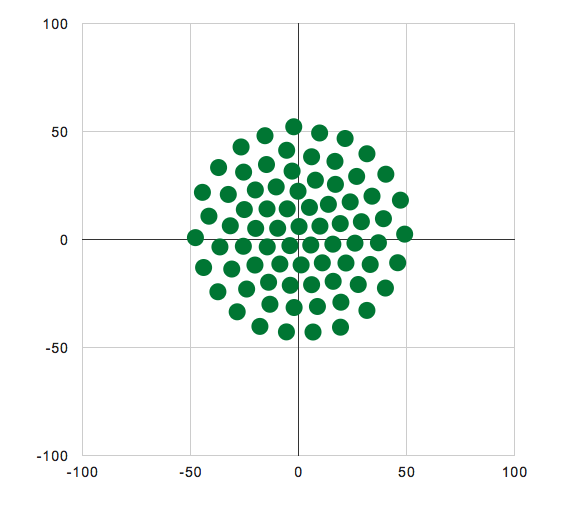
幾何的モデル

粒子配置

Tips

微分方程式の再帰的数値計算において精度を指定する方法

URLの末尾に「?level=4」というように指定することで再帰的に数値を計算している微分方程式について精度を指定できます。「level=」の後につける数値が1増えるたびに精度は2倍になります。デフォルトは4に設定されていて、これは再帰的計算の時間ステップを2-4=1/16としていることになります。level=2であれば、2-2=1/4となります。この値に大きすぎる値を入れると計算に非常に長い時間がかかります。すなわち、数字が１大きくなるごとにおよそ2倍の時間がかかるので、5以下を目安に設定することを強くお勧めします。なお、解析解が求まる微分方程式についてはこのオプションは精度に影響を与えません。

さらに、ロトカ-ボルテラ方程式と、そのロジスティックベースバージョンでは保存量が存在することを確かめやすくするために、プロットする点の数は増やさずに、内部的に精度を上げるオプションを用意しました。URLの末尾に「?inner=4」というように指定することで使用できますが、levelオプションと併用する場合には、「?level=4&inner=2」というように指定してください。levelオプションと同様に1増やすごとに精度が2倍になります。内部的に精度を上げない場合には0を指定します。このオプションではプロットする点の数が少なくすむため、levelオプションと比較して処理時間が短くすみます。デフォルトは5です。この2つの微分方程式以外に対してはinnerオプションは無効です。