非線形回帰
xとyの間に非線形の関係がある場合にも、Rはパラメーターの推定を行うことができます。このページで使用するデータとして、ロジスティック成長曲線に従う誤差を伴ったデータを生成します。ロジスティック成長曲線の解は、xt=K/(1+(K/x0-1)e-rtであるため、K=a、K/x0-1=b、r=cとして、y=a/(1+be-ct)と変形した式のパラメーターa・b・cを推定することにしましょう。
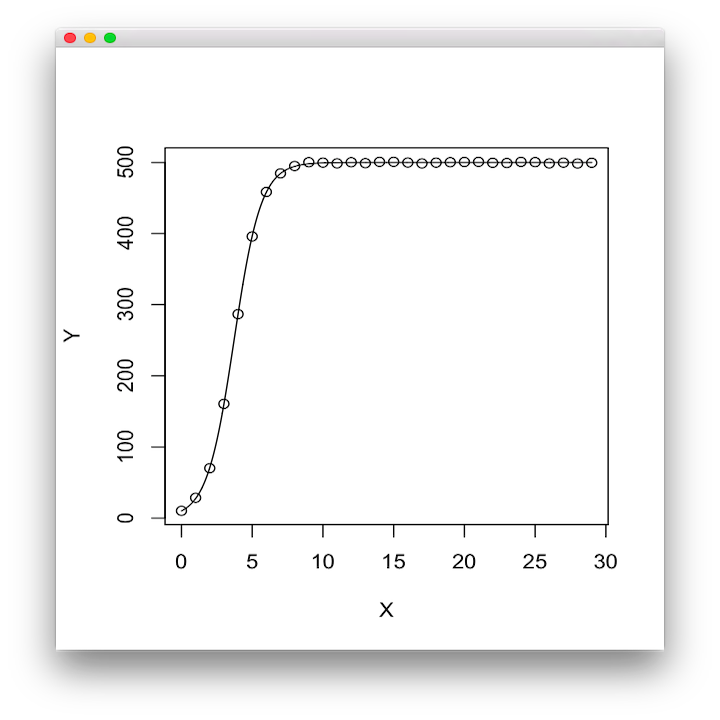
a=500; b=49; c=1.05 x <- seq(0,29,1) #0から29までの1刻みの値をxに格納 y <- a/(1+b*exp(-1*c*x)) + rnorm(30, 0, 1) xy <- data.frame(X=x,Y=y) plot(xy)
nls関数を使って非線形回帰を行う
以下のようにコマンドを打つことにより回帰を行うことができます。初期値を設定していますが、うまく設定しないとエラーが出るため、うまくいかない場合には幾つかの初期値を試してみてください。
xy.nls <- nls(Y~a_/(1+b_*exp(-1*c_*X)),data=xy,start=list(a_=400, b_=40, c_=1.5)) summary(xy.nls)
summary関数により、以下のように出力されます。
Formula: Y ~ a_/(1 + b_ * exp(-1 * c_ * X))
Parameters:
Estimate Std. Error t value Pr(>|t|)
a_ 5.000e+02 1.873e-01 2669.16 <2e-16 ***
b_ 4.917e+01 7.898e-01 62.25 <2e-16 ***
c_ 1.048e+00 4.207e-03 249.06 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8843 on 27 degrees of freedom
Number of iterations to convergence: 7
Achieved convergence tolerance: 1.059e-06
a=500.0、b=49.17、c=1.048というように回帰されました。係数はどれも0.1%有意であることもわかります。最後に、厳密には折れ線グラフとなりますが、近似曲線としてプロットします。
x2 <- seq(0, 29, length=2000) lines(x2, predict(xy.nls, newdata=data.frame(X=x2)))