Masting Year
Beech is the trees that give the acorn. Some years, beech fruits a lot, and other years non. Years of good harvest caused by synchronization of producing seeds are called masting year. They invest too large amount of resource, they are tired to produce seeds next year. Also, they flower all together in a group. There are relatively many tree species which flower and fruit all together in a group. The reason that this strategy evolves is assumed that the efficiency of pollination will increase by flowering all at once . This time we will continue to the simulation in accordance with this model. Since it has posted the source code of C++ at the end of this page, You can refer to it.
About the Model
First, this model assumes the compartment in the forest that can grow N number of trees. There we grow trees only one individual. The trees have respectively the value Y of nutritional status. Trees can produce seeds only when the Y is a positive value. This value is accumulated by 1 per year in the assimilation by photosynthesis. Although the young tree have the setting of they does not bear fruit, only mature trees will bear fruit if they have positive Y value. When trees fruit, Y is reduced.
If k is large, there will be explicit existence of fruiting year and non-fruiting year. On the contrary, small k near to 1 means every-year fruition. Whether the masting evolves or not is assumed to be determined by the parameters of Cross-fertilization dependency, beta, and survival rate of seeds (seedlings), S. This model refers to the paper by Yuuya Tachiki、Yoh Iwasa, Both seedling banks and specialist seed predators promote the evolution of synchronized and intermittent reproduction (masting) in trees (Abstract). You should also read it.
When strong cross-pollen dependency and the high seed survival rate, masting evolves
When you set the parameter like Beta=2.0 and S=0.8, the value k increase year by year, and it means masting evolves.
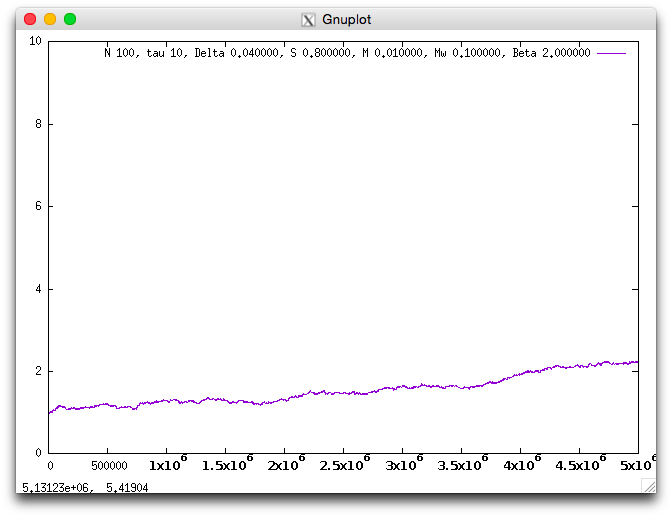
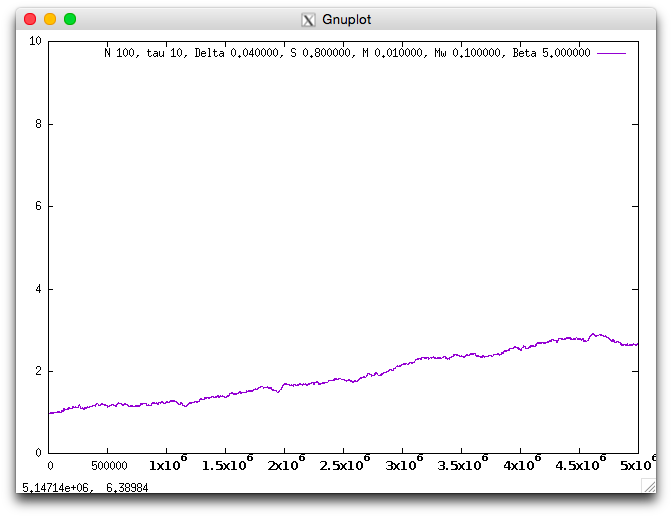
Smaller Bata suppress the masting evolution
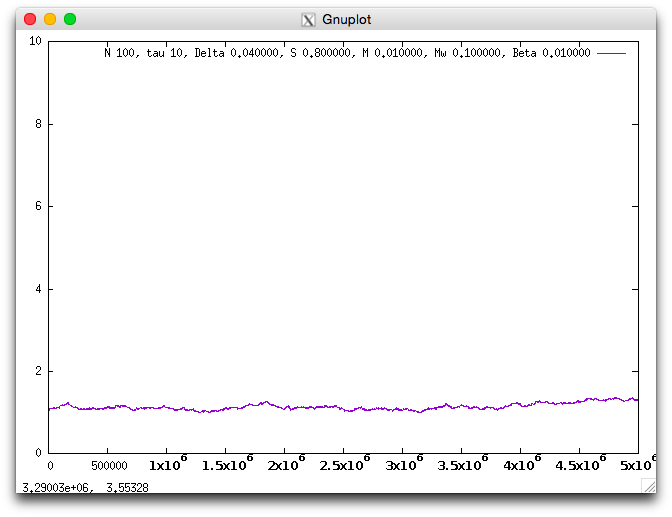
When Beta is small, masting does not evolve because trees can produce seeds whthout others' pollen. It is not necessary to flowering in focus on other individuals' flowering. The value k has converged to a value smaller than the previous example.
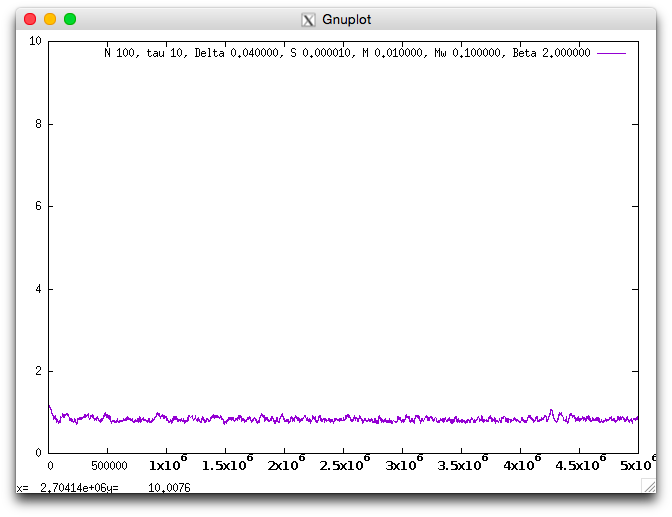
Smaller S suppress the masting evolution
when S is close to 0, masting does not evolves because if it is possible to make a lot of seeds by a enough pollen by synchronizing other individuals, however, the number of seeds of other individuals in this year are as well many so the advantage will be canceled out by the intense competition.
Source Code
This source code is protected by the GNU GPL license. Please visit here for the terms of the GNU GPL license.
This code uses Mersenne Twister for random numbers.The source for Mersenne Twister is here. Also you can get header file, MT.h here.
//
// masting_simulation
//
// Copyright 2015 Yuki Mochizuki
//
#define Year 10000000
#define N 100
#define Tau 10
#define Delta 0.04
#define S 0.0
#define Beta 2.0
#define M 0.01
#define M_width 0.1
#define MeanSeedPerYear 1
#include <iostream>
#include <math.h>
#include <vector>
#include "MT.h"
using namespace std;
class seed
{
public:
double k;
int age;
seed(){
k=1;
age=0;
}
};
int main() {
char *output ="masting_simulation.txt";
FILE* fpo;
fpo=std::fopen( output, "w" );
fprintf(fpo, "N %d, tau %d, Delta %f, S %f, M %f, Mw %f, Beta %f",N,Tau,Delta,S,M,M_width,Beta);
init_genrand(789749);
//data storage
int theta[N];
double k[N];
double Y[N];
int Yp[N];
double P[N];
int age[N];
vector<seed> seeds;
vector<seed> tmp_seeds;
vector<double> pollen_pool;
//temporal variables
int i=0,j=0,pollen=0,recuruit=0;
int seednum[N];
int seed_num=0,pollen_num=0,Yp_count=0;
double k_mean=0,age_mean=0;
seed seed;
//initiate
for(i=0;i<N;i++){
theta[i]=2;
Y[i]=(genrand_real2()-0.5)*3;
k[i]=genrand_real2()+0.5;
age[i]=(int)(genrand_real2()*100.0);
if(age[i]>Tau)theta[i]=2;
else theta[i]=1;
}
for(int y=0;y<Year;y++){
//growth phase
for(i=0;i<N;i++){
Y[i]++;
}
//reproduction phase
pollen=0;
for(i=0;i<N;i++){
if(Y[i]>0)Yp[i]=Y[i];
else Yp[i]=0;
}
for(i=0;i<N;i++){
pollen+=(theta[i]==2)*Yp[i];
}
for(i=0;i<N;i++){
P[i]=pow((double)(pollen-Yp[i])/(double)(N-1),Beta);
}
vector<double>().swap(pollen_pool);
for(i=0;i<N;i++){
seednum[i]=k[i]*P[i]*Yp[i];
for(j=0;j<seednum[i];j++){
pollen_pool.push_back(k[i]);
}
}
pollen_num=pollen_pool.size();
for(i=0;i<N;i++){
Y[i]-=seednum[i];
for(j=0;j<seednum[i]*MeanSeedPerYear;j++){
if(genrand_real2()<M){
seed.k=0.5*(k[i]+pollen_pool.at((int)(genrand_real2()*pollen_num)))+(genrand_real2()-0.5)*2*M_width;
seeds.push_back(seed);
}else{
seed.k=0.5*(k[i]+pollen_pool.at((int)(genrand_real2()*pollen_num)));
seeds.push_back(seed);
}
}
}
seed_num=(int)seeds.size();
//death and recruitment phase
for(i=0;i<N;i++){
if(theta[i]==0||genrand_real2()<Delta){
if(seed_num>0){
recuruit=(int)((double)seed_num*genrand_real2());
k[i]=seeds.at(recuruit).k;
Y[i]=0;
age[i]=0;
theta[i]=1;
}else{
theta[i]=0;
}
}
}
//seed death phase
if(seed_num>0){
vector<class seed>().swap(tmp_seeds);
for(i=0;i<seed_num;i++){
if(genrand_real2()<S){
tmp_seeds.push_back(seeds.at(i));
}
}
vector<class seed>().swap(seeds);
seeds=tmp_seeds;
}
//age
for(i=0;i<N;i++){
if(theta[i]>0)age[i]++;
if(age[i]>Tau)theta[i]=2;
}
//output
if(y%1000==0){
k_mean=0;
age_mean=0;
Yp_count=0;
for(i=0;i<N;i++){
if(theta[i]>0){
k_mean+=k[i];
age_mean+=age[i];
if(Y[i]>0)Yp_count++;
}
}
k_mean/=(double)N;
age_mean/=(double)N;
cout << "Year=" << y << " k(mean)=" << k_mean << " age(mean)=" << age_mean << " seeds=" << seed_num << " fruit=" << Yp_count<< endl;
fprintf(fpo, "%d %f %f %d %d\n",y,k_mean,age_mean,seed_num,Yp_count);
fflush(fpo);
}
}
return 0;
}